Пусть
окружность имеет радиус
,
а ее центр находится в точке
.
Точка
лежит на окружности тогда и только
тогда, когда модуль вектора
равен
,
то есть.
Последнее равенство выполнено тогда и
только тогда, когда
Уравнение (1) и является искомым уравнением окружности.
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору
перпендикулярно вектору
.
Точка
и
перпендикулярны. Векторы
и
перпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю, то есть
.
Используя формулу вычисления скалярного
произведения векторов, заданных своими
координатами, уравнение искомой прямой
записываем в виде
Рассмотрим пример. Найти уравнение прямой, проходящей через
середину отрезка АВ перпендикулярно этому отрезку если координаты точек соответственно равны А(1;6), В(5;4).
Будем
рассуждать следующим образом. Чтобы
найти уравнение прямой мы должны знать
точку, через которую эта прямая проходит,
и вектор перпендикулярный этой прямой.
Вектором, перпендикулярным данной
прямой, будет вектор
,
поскольку, по условию задачи, прямая
перпендикулярна отрезку АВ. Точку
определим
из условия, что прямая проходит через
середину АВ. Имеем
.
Таким образом
и уравнение примет вид.
Выясним вопрос, проходит ли эта прямая через точку М(7;3).
Имеем , значит, эта прямая не проходит через указанную точку.
Уравнение прямой, проходящей через данную точку, параллельно данному вектору
Пусть
прямая проходит через точку
параллельно вектору
.
Точка
лежит на прямой тогда и только тогда,
когда векторы
и
колинеарны. Векторы
и
колинеарны тогда и только тогда, когда
их координаты пропорциональны, то есть
(3)
Полученное уравнение и является уравнением искомой прямой.
Уравнение (3) представим в виде
,
где
принимает любые значения
.
Следовательно, можем записать
,
где
(4)
Система уравнений (4) называется параметрическими уравнениями прямой.
Рассмотрим
пример.
Найти
уравнение прямой, проходящей через
точки
.
Мы можем построить уравнение прямой,
если знаем точку и параллельный или
перпендикулярный ей вектор. Точек в
наличии целых две. Но если две точки
лежат на прямой, то вектор, их соединяющий
будет параллелен этой прямой. Поэтому
воспользуемся уравнением (3), взяв в
качестве вектора
вектор
.
Получаем
(5)
Уравнение (5) называется уравнением прямой, проходящей через две данные точки.
Общее уравнение прямой
Определение.
Общим
уравнением линии первого порядка на
плоскости называется уравнение вида
,
где
.
Теорема. Всякая прямая на плоскости может быть задана в виде уравнения линии первого порядка, и всякое уравнение линии первого порядка является уравнением некоторой прямой на плоскости.
Первая
часть этой теоремы доказывается просто.
На всякой прямой можно указать некоторую
точку
перпендикулярный
ей вектор
.
Тогда, согласно (2), уравнение такой
прямой имеет вид.
Обозначим
.
Тогда уравнение примет вид
.
Теперь
перейдем ко второй части теоремы. Пусть
имеется уравнение
,
где
.
Будем считать для определенности
.
Перепишем уравнение в виде:
;
Рассмотрим
на плоскости точку
,
где
.
Тогда полученное уравнение имеет вид
,
и является уравнением прямой, проходящей
через точку
перпендикулярно вектору
.
Теорема доказана.
В процессе доказательства теоремы мы попутно доказали
Утверждение.
Если имеется уравнение прямой вида
,
то вектор
перпендикулярен данной прямой.
Уравнение
вида
называется общим уравнением прямой на
плоскости.
Пусть
имеется прямая
и точка
.
Требуется определить расстояние от
указанной точки до прямой.
Рассмотрим
произвольную точку
на прямой. Имеем
.
Расстояние
от точки
до прямой равно модулю проекции вектора
на вектор
,
перпендикулярный данной прямой. Имеем
,
преобразуя, получаем формулу:
Пусть даны две прямые, заданные общими уравнениями
,
. Тогда векторы
перпендикулярны первой и второй прямой
соответственно. Угол
между прямыми равен углу между векторами
,
.
Тогда формула для определения угла между прямыми имеет вид:
.
Условие перпендикулярности прямых имеет вид:
.
Прямые
параллельны или совпадают тогда и только
тогда, когда векторы
колинеарны. При этомусловие
совпадения прямых имеет вид
:
,
а
условие отсутствия пересечения
записывается в виде:
.
Последние два условия докажите
самостоятельно.
Исследуем характер поведения прямой по ее общему уравнению.
Пусть
дано общее уравнение прямой
.
Если
,
то прямая проходит через начало координат.
Рассмотрим
случай, когда ни один из коэффициентов
не равен нулю
.
Уравнение перепишем в виде:
,
,
Где
.
Выясним смысл параметров
.
Найдем точки пересечения прямой с осями
координат. При
имеем
,
а при
имеем
.
То есть
- это отрезки, которые отсекает прямая
на координатных осях.Поэтому
уравнение
называется
уравнением прямой в отрезках.
В
случае
имеем
.
В случае
имеем
.
То есть прямая будет параллельна оси
.
Напомним,
что угловым
коэффициентом прямой
называется тангенс угла наклона этой
прямой к оси
.
Пусть прямая отсекает на оси
отрезок
и имеет угловой коэффициент
.
Пусть точка
лежит на данной
Тогда
=
=
.
И уравнение прямой запишется в виде
.
Пусть
прямая проходит через точку
и имеет угловой коэффициент
.
Пусть точка
лежит на этой прямой.
Тогда
=
.
Полученное уравнение называется уравнением прямой, проходящей через данную точку с заданным угловым коэффициентом.
Пусть
даны две прямые
,
.
Обозначим
- угол между ними. Пусть
,
углы наклона к оси Х соответствующих
прямых
Тогда
=
,
.
Тогда
условие параллельности прямых имеет
вид
,
а условие перпендикулярности
В заключение рассмотрим две задачи.
Задача . Вершины треугольника АВС имеют координаты: A(4;2), B(10;10), C(20;14).
Найти: а) уравнение и длину медианы, проведенной из вершины А;
б) уравнение и длину высоты, проведенной из вершины А;
в) уравнение биссектрисы, проведенной из вершины А;
Определим уравнение медианы АМ.
Точка М() середина отрезка ВС.
Тогда
,
.
Следовательно, точка М имеет координаты
M(15;17).
Уравнение медианы на языке аналитической
геометрии это уравнение прямой, проходящей
через точку А(4;2) параллельно вектору
={11;15}.
Тогда уравнение медианы имеет вид.
Длина медианы АМ=
.
Уравнение высоты AS - это уравнение прямой, проходящей через точку А(4;2) перпендикулярно вектору ={10;4}. Тогда уравнение высоты имеет вид 10(x-4)+4(y-2)=0, 5x+2y-24=0.
Длина
высоты - это расстояние от точки А(4;2) до
прямой ВС. Данная прямая проходит через
точку B(10;10)
параллельно вектору
={10;4}.
Ее уравнение имеет вид
,
2x-5y+30=0.
Расстояние AS
от точки А(4;2) до прямой ВС, следовательно,
равно AS=
.
Для определения уравнения биссектрисы найдем вектор параллельный этой прямой. Для этого воспользуемся свойством диагонали ромба. Если от точки А отложить единичные векторы одинаково направленные с векторамии, то вектор, равный их сумме, будет параллелен биссектрисе. Тогда имеем=+.
={6;8},
,
={16,12},
.
Тогда
=
В качестве направляющего вектора искомой
прямой может служить вектор={1;1},
коллинеарный данному. Тогда уравнение
искомой прямой имеет видилиx-y-2=0.
Задача. Река протекает по прямой линии, проходящей через точки А(4;3) и В(20;11). В точке С(4;8) живет Красная Шапочка, а в точке D(13;20) ее бабушка. Каждое утро Красная Шапочка берет пустое ведро из дома, идет на реку, черпает воду и относит ее бабушке. Найти самую короткую дорогу для Красной Шапочки.
Найдем точку Е, симметричную бабушке, относительно реки.
Для этого сначала найдем уравнение прямой, по которой течет река. Это уравнение можно рассматривать, как уравнение прямой, проходящей через точку А(4;3) параллельно вектору . Тогда уравнение прямой АВ имеет вид.
Далее
найдем уравнение прямой DE,
проходящей через точку D
перпендикулярно АВ. Его можно рассматривать,
как уравнение прямой, проходящей через
точку D,
перпендикулярно вектору
.
Имеем
Теперь найдем точку S - проекцию точки D на прямую АВ, как пересечение прямых АВ и DE. Имеем систему уравнений
.
Следовательно, точка S имеет координаты S(18;10).
Поскольку S середина отрезка DE, то .
Аналогично .
Следовательно, точка Е имеет координаты Е(23;0).
Найдем уравнение прямой СЕ, зная координаты двух точек этой прямой
Точку М найдем как пересечение прямых АВ и СЕ.
Имеем систему уравнений
.
Следовательно,
точка М имеет координаты
.
Тема 2. Понятие об уравнении поверхности в пространстве. Уравнение сферы. Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору. Общее уравнение плоскости и его исследование Условие параллельности двух плоскостей. Расстояние от точки до плоскости. Понятие об уравнении линии. Прямая линия в пространстве. Канонические и параметрические уравнения прямой в пространстве. Уравнения прямой, проходящей через две данные точки. Условия параллельности и перпендикулярности прямой и плоскости.
Вначале, дадим определение понятия уравнения поверхности в пространстве.
Пусть
в
пространстве
задана некотораяповерхность
.
Уравнение
называется уравнениемповерхности
,
если выполнены два условия:
1.для
любой точки
с координатами
,
лежащей наповерхности,
выполнено
,
то есть ее координаты удовлетворяют
уравнениюповерхности;
2.
любая точка
,
координаты которой удовлетворяют
уравнению
,
лежит на линии.
Определение 1 . Числовой осью (числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
O → x
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины .
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат , не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату , которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA 1 и AA 2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A 1 на числовой оси Ox , ординатой точки A называют координату точки A 2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y ) или A = (x ; y ).
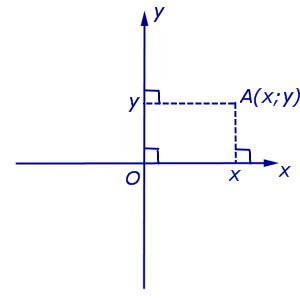
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти (квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Утверждение 1 . Расстояние между двумя точками координатной плоскости
A 1 (x 1 ; y 1) и A 2 (x 2 ; y 2)
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
Уравнение линии на плоскости
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Определение 1
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ -- произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Уравнение прямой.
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ - серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\{x,y\}$, принадлежащую прямой $l$ (рис. 3).
Так как прямая $l$ - серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Следовательно
Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c={x_2}^2+{y_2}^2-{x_1}^2-{y_1}^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:
Пример задачи на нахождение уравнений линий в декартовой системе координат
Пример 1
Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим
\[{(x-2)}^2+{(y-4)}^2=r^2\]
Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$
Получаем, уравнение окружности имеет вид:
\[{(x-2)}^2+{(y-4)}^2=20\]
Найдем теперь уравнение окружности, используя частный случай 1. Получим
Тема урока: Уравнение окружности
Цели урока:
Образовательные: Вывести уравнение окружности, рассмотрев решение этой задачи как одну из возможностей применения метода координат.
Уметь:
– Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.
Воспитательные : Формирование критического мышления.
Развивающие : Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
Уметь:
– Видеть проблему и наметить пути её решения.
– Кратко излагать свои мысли устно и письменно.
Тип урока: усвоения новых знаний.
Оборудование : ПК, мультимедийный проектор, экран.
План урока:
1. Вступительное слово – 3 мин.
2. Актуализация знаний – 2 мин.
3. Постановка проблемы и её решение –10 мин.
4. Фронтальное закрепление нового материала – 7 мин.
5. Самостоятельная работа в группах – 15 мин.
6. Презентация работы: обсуждение – 5 мин.
7. Итог урока. Домашнее задание – 3 мин.
Ход урока
Цель данного этапа: Психологический настрой учащихся; Вовлечение всех учащихся в учебный процесс, создание ситуации успеха.1. Организационный момент.
3 минуты
Ребята! С окружностью вы познакомились ещё в 5 и 8 классах. А что вы о ней знаете?
Знаете вы много, и эти данные можно использовать при решении геометрических задач. Но для решения задач, в которых применяется метод координат, этого недостаточно. Почему?
Абсолютно верно.
Поэтому главной целью сегодняшнего урока я ставлю выведение уравнения окружности по геометрическим свойствам данной линии и применение его для решения геометрических задач.
И пусть девизом урока станут слова среднеазиатского учёного-энциклопедиста Ал-Бируни: «Знание - самое превосходное из владений. Все стремятся к нему, само же оно не приходит».
Записывают тему урока в тетрадь.
Определение окружности.
Радиус.
Диаметр.
Хорда. И т.д.
Мы ещё не знаем общего вида уравнения окружности.
Учащиеся перечисляют все, что знают об окружности.
Слайд 2
Слайд 3
Цель этапа – получить представление о качестве усвоения учащимися материала, определить опорные знания.
2. Актуализация знаний.
2 минуты
При выведении уравнения окружности вам потребуются уже известное определение окружности и формула, позволяющая найти расстояние между двумя точками по их координатам. Давайте вспомним эти факты /п овторение материала, изученного ранее/:
– Запишите формулу нахождения координат середины отрезка.
– Запишите формулу вычисления длины вектора.
– Запишите формулу нахождения расстояния между точками (длины отрезка).
Корректирование записей…
Геометрическая разминка.
Даны точки А (-1;7) и В (7; 1).
Вычислите координаты середины отрезка АВ и его длину.
Проверяет правильность выполнения, корректирует расчеты…
Один ученик у доски, а остальные в тетрадях записывают формулы
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
|АВ|=√(х –х)²+(у –у)²
М(х;у), А(х;у)
Вычисляют: С (3; 4)
| АВ| = 10
С лайд 4
Слайд 5
3. Формирование новых знаний.
12 минут
Цель: формирование понятия - уравнение окружности.
Решите задачу:
В прямоугольной системе координат построена окружность с центром А(х;у). М(х; у) - произвольная точка окружности . Найдите радиус окружности.
Будут ли координаты любой другой точки удовлетворять данному равенству? Почему?
Возведём обе части равенства в квадрат. В результате имеем:
r² =(х –х)²+(у –у)²-уравнение окружности, где (х;у)-координаты центра окружности, (х;у)-координаты произвольной точки лежащей на окружности, r-радиус окружности.
Решите задачу:
Какой вид будет иметь уравнение окружности с центром в начале координат?
Итак, что надо знать для составления уравнения окружности?
Предложите алгоритм составления уравнения окружности.
Вывод: … записать в тетрадь.
Радиусом называется отрезок, соединяющий центр окружности с произвольной точкой лежащей на окружности. Поэтому r=|АМ|=√(х –х)²+(у –у)²
Любая точка окружности лежит на этой окружности.
Учащиеся ведут записи в тетради.
(0;0)-координаты центра окружности.
х²+у²=r², где r-радиус окружности.
Координаты центра окружности, радиус, любую точку окружности…
Предлагают алгоритм…
Записывают алгоритм в тетрадь.
Слайд 6
Слайд 7
Слайд 8
Учитель фиксирует равенство на доске.
Слайд 9
4. Первичное закрепление.
23 минуты
Цель: воспроизведение учащимися только что воспринятого материала для предупреждения утраты образовавшихся представлений и понятий . Закрепление новых знаний, представлений, понятий на основе их применения.
Контроль ЗУН
Применим полученные знания при решении следующих задач.
Задача: Из предложенных уравнений назовите номера тех, которые являются уравнениями окружности. И если уравнение является уравнением окружности, то назовите координаты центра и укажите радиус.
Не каждое уравнение второй степени с двумя переменными задаёт окружность.
4х²+у²=4- уравнение эллипса.
х²+у²=0- точка.
х²+у²=-4- это уравнение не задаёт никакой фигуры.
Ребята! А что нужно знать, чтобы составить уравнение окружности?
Решите задачу №966 стр.245(учебник).
Учитель вызывает ученика к доске.
Достаточно ли данных, которые указаны в условии задачи, чтобы составить уравнение окружности?
Задача:
Напишите уравнение окружности с центром в начале координат и диаметром 8.
Задача : построение окружности.
Центр имеет координаты?
Определите радиус… и выполняйте построение
Задача на стр.243 (учебник) разбирается устно.
Используя план решения задачи со стр.243, решите задачу:
Составьте уравнение окружности с центром в точке А(3;2), если окружность проходит через точку В(7;5).
1) (х-5)²+(у-3)²=36- уравнение окружности;(5;3),r=6.
2) (х-1)²+у²=49- уравнение окружности;(1;0),r=7.
3) х²+у²=7- уравнение окружности;(0;0),r=√7.
4) (х+3)²+(у-8)²=2- уравнение окружности; (-3;8),r=√2.
5) 4х²+у²=4-не является уравнением окружности.
6) х²+у²=0- не является уравнением окружности.
7) х²+у²=-4- не является уравнением окружности.
Знать координаты центра окружности.
Длину радиуса.
Подставить координаты центра и длину радиуса в уравнение окружности общего вида.
Решают задачу № 966 стр.245(учебник).
Данных достаточно.
Решают задачу.
Так как диаметр окружности в два раза больше её радиуса, то r=8÷2=4. Поэтому х²+у²=16.
Выполняют построение окружностей
Работа по учебнику. Задача на стр.243.
Дано: А(3;2)-центр окружности; В(7;5)є(А;r)
Найти: уравнение окружности
Решение: r² =(х –х)²+(у –у)²
r² =(х –3)²+(у –2)²
r = АВ, r² = АВ²
r² =(7-3)²+(5-2)²
r² =25
(х –3)²+(у –2)²=25
Ответ: (х –3)²+(у –2)²=25
Слайду 10-13
Решение типовых задач, проговаривая способ решения в громкой речи.
Учитель вызывает одного ученика записать полученное уравнение.
Возврат к слайду 9
Обсуждение плана решения данной задачи.
Слайд. 15. Учитель вызывает одного ученика к доске решать данную задачу.
Слайд 16.
Слайд 17.
5. Итог урока.
5 минут
Рефлексия деятельности на уроке.
Домашнее задание: §3, п.91, контрольные вопросы №16,17.
Задачи № 959(б, г, д), 967.
Задача на дополнительную оценку (проблемная задача): Построить окружность, заданную уравнением
х²+2х+у²-4у=4.
О чём на уроке мы говорили?
Что хотели получить?
Какая цель была поставлена на уроке?
Какие задачи позволяет решить сделанное нами «открытие»?
Кто из вас считает, что достиг цели, поставленной на уроке учителем на100%, на 50%; не достиг цели…?
Выставление оценок.
Записывают домашнее задание.
Учащиеся отвечают на поставленные учителем вопросы. Проводят самоанализ собственной деятельности.
Учащимся необходимо выразить в слове результат и способы достижения.